论文摘趣第二期（说好的周更呢？！），我们来对图像去雾算法做一个简短的综述。图像去雾是一个公认的比较困难的问题，甚至在很多情况下是一个欠适定（underdetermined）的问题（从下文的成像模型可以看出）。因此有不少工作是利用多张图片或者额外信息来实现去雾效果的。然而本文关注的焦点在于单张图像的去雾算法（single image dehazing），即给定一张含有雾气的图像，我们希望还原其无雾的图像。

一、有雾图像的成像模型

在计算机视觉和图形学领域中，人们对有雾图像的形成原理有一个常用的物理模型——大气散射模型（atmospheric scattering model）。为了保持符号的一致，我们以下统一采用“暗通道先验”文章中的表示方式。

大气散射模型首先基于这样的一个现象：光线经过一个散射媒介之后，其原方向的光线强度会受到衰减，并且其能量会发散到其他方向。因此，在一个有雾的环境中，相机（或者人眼）接收到的某个物体（或场景）的光其实来源于两个部分：1、来自于该物体（或场景）本身，这个部分的光强受到散射媒介的影响会有衰弱；2、来自大气中其他光源散射至相机（或人眼）的光强。见下图：

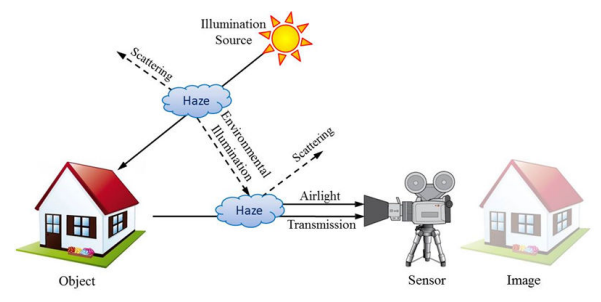来源：DehazeNet: An End-to-End System for Single Image Haze Removal

由于能量是守恒的，散射掉的部分光强度应该跟其他光源散射过来的光强是一样的。因此，我们可以将一张有雾的图像表示为以下的一个线性模型：

其中 \( I(x) \) 是有雾图像，\( J(x) \) 是物体（或场景）的原始辐射（radiance），\(A\) 是全局大气光照，\( t(x) \) 被称作介质透射率（medium transmission）。其中第一项 \( J(x)t(x) \) 又称作直接衰减（direct attenuation）；第二项 \( A(1-t(x)) \) 称作 airlight。由于大气的全局光照应该是无向且均匀的，我们可以把 \( A \) 近似为一个于位置无关的常量，而透射率 \( t(x) \) 则是与位置相关的，因此是一个二维的透射图。

再进一步，如果我们假设大气是均质（homogenous）的话，透射率则与物体（或场景）到相机的距离成反指数关系：

其中 \( d(x) \) 是深度图（depth map），\( \beta \) 是大气的散射系数。

从几何上看，上文的大气散射模型说明了在 RGB 颜色空间当中，向量 \( A \)、\( I(x) \) 和 \( J(x) \) 是共面的，而且它们的终点应该是共线的，透射率 \( t(x) \) 是 \( \left\lVert A-I(x)\right\rVert \) 和 \( \left\lVert A-J(x)\right\rVert \) 的比值。如下图：

来源：Single Image Haze Removal Using Dark Channel Prior

另外从公式中我们可以看到，当距离趋近于无穷大，即 \( d(x) \) -> \( inf \) 时，我们有 \( A=I(x) \)。虽然实际中距离不可能是无穷大的，但是我们可以利用这一性质来估计大气的全局光照，即找到透射率最小（雾气最浓）的位置的最大光照强度：\( A = \max_{y\in \{x|t(x)\leq t_0 \}}I(y) \)。

有了\( I(x) \)、\( t(x) \) 和 \( A \)，我们就可以利用大气散射模型公式还原出 \( J(x) \)：

然而，如果只提供单张图像的信息的话，同时求解 \( J(x) \)、\( t(x) \) 和 \( A \) 是一个欠适定的问题。因为对于每个像素点，我们可以得到三个方程式（分别对应三个颜色通道），但我们一共要求解四个未知数（即便假设 \( A \) 可以估计得到）。因此，人们往往需要利用各种先验知识（如暗通道先验）来先估计透射图 \( t(x) \)，并以此求出其他未知量。

二、文献一览

2008年

2008年巧合般地出现了两篇关于单张图像去雾算法的经典论文，它们都具有开创性的意味，引用率很高。颇为有趣的是，这两篇文章都是单一作者署名的。

用MRF建模，最大化局部对比度

为了解决单张图像去雾这个 ill-posed 的问题，我们往往需要加入一些先验知识，而这篇文章中用到的先验知识便是图像的对比度（contrast）。该算法有三个假设：1、有雾图像的对比度比无雾图像的对比度低；2、透射率（与原文中的量略有不同，但本质是一样的）的变化只与物体（或场景）的深度有关，因此局部区域内的透射率是接近恒定的，而且除了少数不连续的像素点意外，相邻区域透射率的变化是平滑的；3、复原之后图像的统计特性应该与实际的无雾照片特性一致（由于该算法只是一种增强对比度的算法，理论上并不是为了直接还原无雾照片，所以引入该假设来说明该算法可以达到近似去雾的效果）。

如果我们将图像的对比度量化为图像的梯度和（可以理解为图像边缘越多对比度越强），那么图像对比度可以表示为：

从上文的大气散射模型可以得到假设1的论点（因为 \(t\leq1\)）：

结合对比度先验和透射率变化平滑的假设，该文章用马尔可夫随机场（Markov Random Field， MRF）对透射图进行建模。其中MRF的势能函数包含两项：1、“数据项”，表示的是局部区域在各个透射率下的对比度（用上文提到的梯度和表示）；2、“平滑项”，表示相邻区域的透射率应该比较相近，是一个正则化项。建模完成后，通过 graph cuts 或者 belief propagation 算法可以求解最大化势能函数时的最优透射率，从而得到估计的透射图 \(t(x)\)。

虽然该算法利用 对比度先验 较为成功地实现了单张图像的去雾，但是它只是一种单纯从 图像增强 角度出发的方法，并没有从物理模型的角度上还原物体（或场景）的辐射，即人们常说的 not physically-grounded。而且该方法往往会得到过饱和的图像。

假设shading和透射率统计独立，运用独立成分分析估计透射图

与前文不同，这篇文章提出了一个基于物理模型的图像去雾方法。首先，文中对场景辐射 \(J(x)\) 作了一定的简化——局部反照率恒定（locally constant albedo）。我们把未知图像 \(J(x)\) 分解为两项相乘的形式 \( R(x)l(x) \)，其中 \(R\) 是一个三通道的RGB向量，代表场景表面的反射系数；\(l(x)\) 是一个标量，表示该位置的反射光强。局部分照率恒定 则是假设一个局部区域内各个像素点的反射系数是一致的：\( R(x) = R, x\in \Omega \)。因此，同一个局部内的所有 \(J(x)\) 都具有相同的方向 \(R\)。如下图：

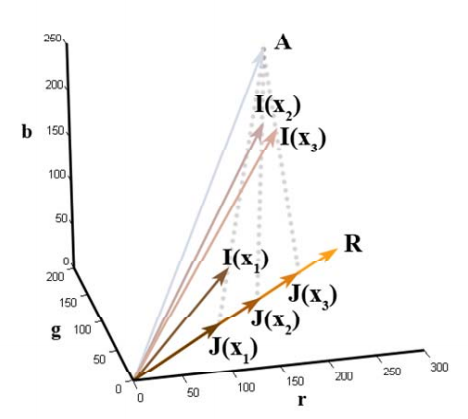来源：Single Image Haze Removal Using Dark Channel Prior

然后，论文提出了一个很重要的假设：场景的表面shading（求翻译）和透射率是统计上独立的。这个假设源于shading \(l(x)\) 取决于场景的照度，表面的反射特性和场景的几何特性；而透射率 \(t(x)\) 取决于场景的深度 \(d(x)\) 和雾的浓度（散射度）\(\beta\)，理论上而言应该是统计独立的。有了这个假设之后，我们就可以通过独立成分分析（Independent Component Analysis）估计出\(l(x)\) 和 \(t(x)\)。

如前所述，这篇文章的方法是基于物理模型的，能得到较好的无雾图像和深度图。然而该方法会受到其“统计独立性”的假设的限制，比如在信噪比较低（浓雾场景）的情况下得到的统计特性会不准确。另外该方法基于颜色信息，对于灰度图或者浓雾场景导致的colorless的情况不太适用。（以上评论来自“Single Image Haze Removal Using Dark Channel Prior”）

2009年

1. Single Image Haze Removal Using Dark Channel Prior (CVPR09, link)

暗通道先验估计透射图

这篇文章可谓是单张图像去雾算法的 seminal work。特别是该文章出自Kaiming He之手，又是当年CVPR的best paper，对于华人CV研究者来说应该是无人不知吧。我个人是真的*非常喜欢读这篇论文的。算法简洁优美而不失广泛性，文章易读清晰而不失全面性，的确不愧为best paper。

暗通道先验的算法十分简单，而且网上介绍这篇论文的文章太多了，所以我也不打算再多赘述了。放个dark channel的计算公式，强烈推荐感兴趣的朋友读读原文。

2014年

利用各种先验作为特征，构建随机森林回归器来估计透射图

暗通道先验算法提出后的几年，大多的后续工作都只是在此基础上的一些（较小的）改进。虽然暗通道先验在很多场景下能得到不错的效果，但如前所述还是有其缺陷的。这篇文章的一个出发点就是，前人工作中的各种先验知识之间可以起到互相补充（complementary）的作用，弥补单一先验特征在某些场景下不适用的问题。那么要如何结合这些不同的先验知识呢？一个直接的思路就是回归了。本文用的便是构建一个随机森林回归器（Random Forest regressor），以各种先验特征为输入，通过随机森林模型估计透射图。我们可以看到，与之前偏向图像处理的工作不同，这个工作将机器学习算法应用到去雾算法当中，希望利用一定量的训练数据自动找到合适的模型来估计透射图。通过训练后发现，暗通道先验特征的确是其中最有信息量的特征。

另外值得一提的是它的训练数据的生成方式，该方法影响了之后很多的利用机器学习实现去雾的算法。由于实际中一般很难得到大量的成对（有雾和无雾）图像来训练网络，文中采用合成的图像（利用大气散射模型）作为训练数据。文中从网上收集部分无雾的照片，从中任意采样16*16的图像块，然后对图像块合成为有雾的图像块。其中合成基于两点假设：1、图像内容如透射率无关（同样的图像内容可以有不同深度的情况）；2、透射率在局部区域内是恒定的（小图像块中的像素点具有相同的深度）。由于这两个假设，我们就可以任意选取一个0到1的值作为某个图像块的 \(t\)，然后以此合成有雾的照片。为了简化学习过程，通常将 \(A\) 设为常数1。

在训练模型中有一个小细节：提取出的先验知识特征往往跟图像内容是十分相关的，这与上面提到的“图像内容如透射率无关”的假设是违背的。为了消除这种相关性的影响，文章在训练时先将提取到的特征进行排序。这样由于位置信息被打乱了，内容的相关性也被打破了。

2015年

构建线性模型，用亮度和饱和度估计场景深度

本文的模型与上一篇十分相似，都是采用一个回归模型对场景深度（前文是透射率）进行估计。不同的是，本文提出了一种新的先验知识：颜色衰减先验。该先验基于一个发现：在无雾区域部分，其亮度（brightness）和颜色饱和度（saturation）应该是相近的；而在有雾区域部分，其亮度和颜色饱和度会相差很多。如下图：

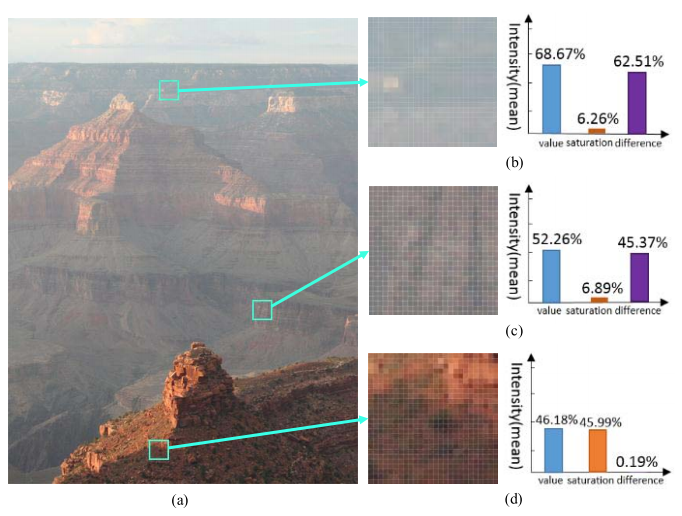来源：A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior

其实这个现象可以通过大气散射模型解释：在雾浓度较高的区域，大气散射到达的光比例就会增多，这会导致颜色都趋近于白色，饱和度下降同时亮度增加。由于雾的浓度与场景深度有关，因此我们可以得出一个结论：场景深度与“亮度和饱和度的差“成正比关系。为了具体表示这个关系，文章采用了一个简单的线性回归模型， 以亮度和饱和度为变量预测场景深度。

2016年

卷积神经网络生成透射图

将卷积神经网络运用到去雾问题（估计透射图）的工作。模型方面，文章中的卷积神经网络只有三层：1、基于 Maxout unit 的“特征提取”层；2、并行使用不同大小卷积核的“多尺度映射”层及之后Maxpooling的“局部最大值”层；3、使用了一个双边ReLU（BReLU）作为激活函数的“非线性回归”层。如下图：

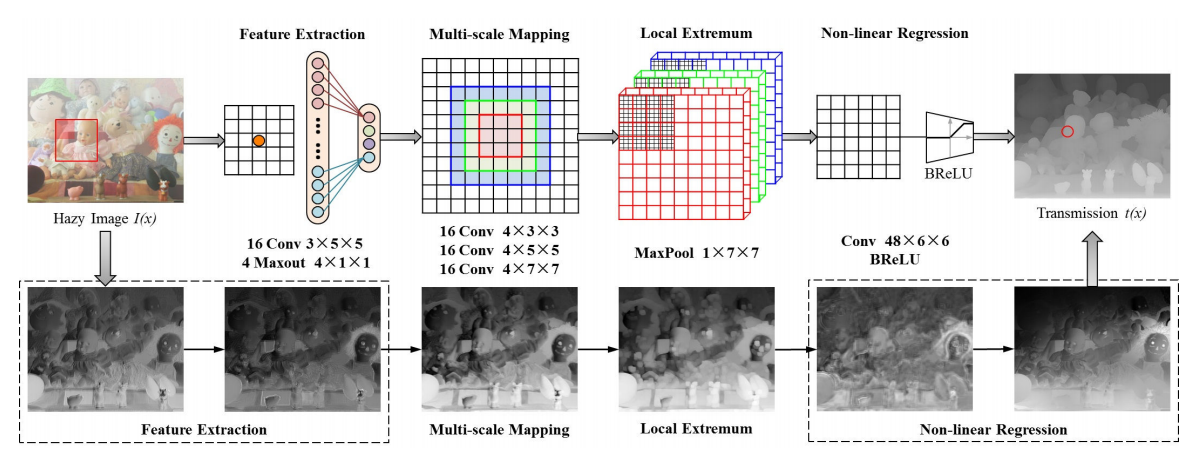来源：DehazeNet: An End-to-End System for Single Image Haze Removal

网络结构非常简单，损失函数也只是MSE loss，然而效果看着还是挺不错的（跑过代码）。

多尺度卷积神经网络生成透射图

与前文非常相似的思路，不同的是提出了一个多尺度的卷积神经网络结构。通过先用粗糙网络生成粗粒度的透射图，再用精细网络进一步得到更细致的图像。网络结构如下：

来源：Single Image Dehazing via Multi-Scale Convolutional Neural Networks

利用全局像素的“雾线”来估计透射图

这是一篇挺有意思的文章，提出了一种基于全局（整张图片像素点）的估计透射图的方法，与以往基于局部区域的估计方法有所不同。首先，文章基于一个先验知识：一张无雾的图像中不同颜色的数量远远低于图像像素点的数量。换句话说，无雾图像可以由少量的（几百种）颜色来近似。这种颜色量化的方法其实在图像压缩等应用中是很常见的。下图是一个例子，我们可以看到将图像颜色量化为500种不同颜色后，其质量并没有太大的改变：

来源：Non-Local Image Dehazing

在RGB空间上看的话，上述现象说明无雾图像中像素点的颜色在RGB空间上可以聚类成几百个紧致的团簇（如下图b）。然而当图像中存在雾时，由于像素值是原像素辐射值与大气光照的凸组合（从大气散射模型可以看出），本来是同一团簇的像素点会分布在RGB空间的一条直线上。其中线段的两头分别是像素的原始辐射值和大气光照（如下图d）。我们把这些线叫做雾线。同时我们可以看到，同一个雾线（或团簇）上的像素点可以来自图像的各个位置，因此该方法是全局的。

来源：Non-Local Image Dehazing

算法的第一步是找到这些雾线，因为他们应该是对应相近的原始辐射值的。唯一导致它们分布不同的原因是：它们位于图像的不同位置、不同的深度，所以会有着不同的透视率。为了找到雾线，文章首先将原图减去全局的大气光照（可以用各种传统方法估计得到）：\(I_A(x)=I(x)-A=t(x)|J(x)-A|\)。这样做的目的是将全局大气光照转移到新坐标的原点。然后再将该坐标转换为球坐标（spherical coordinates），其中包含三个维度：径向距离 \(r(x)\)，天顶角 \(\theta (x)\) 和方位角 \(\phi (x)\)。这样我们可以发现，由 \(t(x)\) 不同而产生的变化只对 \(r(x)\) 有影响而不会改变 \(\theta (x)\) 和 \(\phi (x)\)。如此一来我们就可以根据 \(\theta (x)\) 和 \(\phi (x)\) 来对像素点聚类从而找到雾线。聚类的方法也非常高效：先在球面上进行均匀采样，然后对采样点建立 KD-Tree 并且以此进行高效的最近邻域查找。

算法的第二步是利用雾线估计透射率。从上面的介绍可以知道，像素点的径向距离取决于该点的透射率：\( r(x) = t(x) \|J(x)-A\|\)。其中当 \(t=1\)时（即无雾区域），\(r(x)\) 会取到最大值 \(r_{max}\)。那么结合前文的式子，我们可以估计出透射率：\(t(x) = r(x) / r_{max}\)。为了从有雾图像中估计出 \(r_{max}\)，文中做了两个假设：1、所有雾线都有一个对应无雾像素的点；2、这个点是雾线中距离全局大气光照最远的点。即 \(\hat{r}_{max}(x) = \max_{x\in H}\{r(x)\} \)，\(H\) 表示某条雾线。综上所述，我们可以得到一个透射率的初步估计：\(\widetilde{t}(x) = r(x) / \hat{r}_{max}\)。

算法的第三步是对透射率的估计做进一步的正则化。正则化包括两部分。其一，我们可以从大气散射模型得到一个对于透射率的下限估计： \( t_{LB}(x) = 1 - \min_{c\in\{R,G,B\}} \{I_c(x)/A_c\} \)，那么透射率应该是初步估计和下限估计的较大值：\( \widetilde{t}_{LB}(x)=\max \{\widetilde{t}(x), t_{LB}(x)\} \)。最后，再加入一个很常用的基于平滑的正则化项：需要优化的目标函数中包含一个与 \(\widetilde{t}_{LB}(x)\) 尽量相近的数据项，以及四邻域内透射率相近的平滑项。

估计出透射率之后，我们就可以用大气散射模型得到去雾后的图像了。这个算法十分直接好懂。由于是基于全局的算法，比之前的方法更为高效和鲁棒。一个缺点是当大气光照比场景亮度强很多的时候，雾线会变得很难检测。

2017年

端到端去雾网络

目前最新publish的去雾算法工作，彻底将去雾问题转化为一个端到端（End-to-End）解决的问题。首先，为了实现端到端训练且避免利用额外的方法估计全局大气光照 \(A\)，文章做了一些简单的数学变换，把 \(t(x)\) 和 \(A\) 统一到了一个变量 \(K(x)\) 当中。这样只需要用网络估计出 \(K(x)\) 就可以直接得到 \(J(x)\) 了。网络结构仍是异常简单（见下图），效果嘛……跟前两个比也没感觉有啥区别。

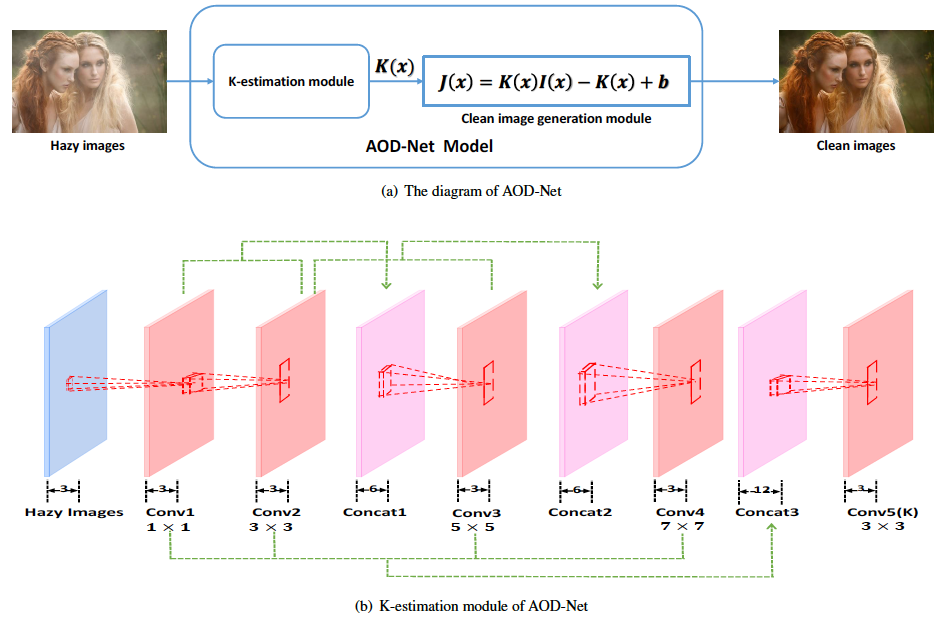来源：AOD-Net: All-in-One Dehazing Network

值得一提的是，其实 \(K(x)\) 里面还包含了 \(I(x)\)，换句话说，个人觉得这跟用网络直接从 \(J(x)\) 估计 \(I(x)\) 的难度没什么区别…另外，文章还把去雾这部分作为一种预处理应用在目标检测当中。

三、小结

简单总结一下。从以上的论文我们可以看到，由于单张图像去雾这个问题本身非常困难，甚至是欠适定的，因此人们通常会依靠各种图像的先验知识（如暗通道、颜色衰减、雾线、对比度等）来辅助估计透射图。同时我们也看到了透射图对去雾算法是否能成功有着重要影响。相比于各种传统的基于先验知识的方法，机器学习甚至深度学习的方法则显得单调得多，也缺乏对问题本身以及图像统计特性十分深刻的理解。不过基于深度学习的方法可以理解为运用了非常强大的非线性模型，利用大量的有／无雾图像的数据对，对透射图进行估计，因此一般能得到超越传统方法的结果。但是这些基于机器学习的算法在不同数据上的泛化性也是一个未知数。而相对的，基于先验知识的方法，只要在其中假设不被破坏的情况下是可以得到不错的结果的。这也是暗通道先验算法至今一直都是作为广义情况下去雾算法的基准的原因。